Modern programming languages abstract a lot of low-level details of how our code works. Nonetheless, a good understanding of underlying computer science concepts can help you write better code… and pass technical interviews 😉 In the previous part of this article we introduced arrays, lists, and dynamic arrays. Now, we will look into the operations they support and how fast those operations are.

In the first part of the article we introduced three fundamental data structures:

• an array — a collection of elements stored in the memory as a single, continuous block of data
• a list — a collection of elements, each containing a link to the next element
• a dynamic array — an array that is resized to fit all elements without wasting too much space

Let’s compare those data structures. What operations do they support? How fast are they?

A basic understanding of time complexity and big-O notation is required as I use them extensively. If you’re not familiar with those concepts, HackerRank has a great video-explanation.

Let’s dig in!

What operations are supported by those data structures? What is their time complexity?

(In this section I denote the size of the array as n)

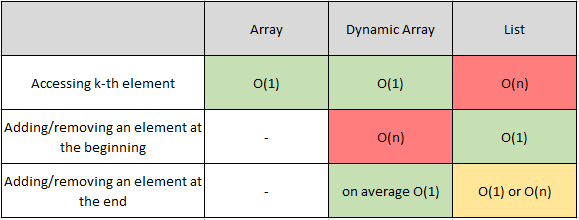
Array

“Vanilla” arrays are dead simple. We can:

• access an element given its index — in O(1) time. We know exactly where each element is located in memory, so we can access it very quickly.

That’s all. We can’t add or remove new elements (arrays always have a constant size).

Dynamic array

Dynamic arrays are more interesting. As with “vanilla” arrays, given an index, we can access a corresponding element in constant time. Dynamic arrays also support adding and removing elements.

Adding an element

• at the end of the list — takes, on average, O(1) time. Remember that some insertions will take O(n) time.
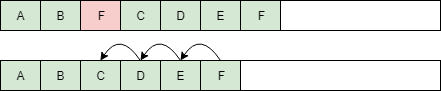
• at the beginning of the list, or somewhere in the middle — takes linear time. To insert a new element in the middle of the list, we have to “shift” all preceding elements by one position (see illustration below). We have to copy a portion of the array — O(n) elements, so this operation takes O(n) time.

Removing an element

• from the end of the list — takes, on average, O(1) time. Again, some insertions are slow and take linear time.
• from somewhere else in the list — takes O(n) time. As with adding an element in the middle, we have to shift all preceding elements — this time in the opposite direction (see illustration below). Thus, removal will take O(n) time.

Linked List

In a linked list, accessing an element with a given index i is a bit more complicated. As we don’t know where that element can be found in memory, we have to iterate through the list until we find it. This will take O(n) time. That’s significantly slower than other data structures we discussed.

Lists allow adding and removing elements too.

Adding an element

• at the beginning of the list - is just a matter of changing a few pointers, so it can be done in O(1) time. We have to change the value of head so that it points to our new element NEW and set NEW.next_element so that it points to A (see illustration below).

• somewhere in the middle — can always be done in O(n) time. First, we need to find the spot where we want to insert the element — this will take O(n). Inserting the element can be done in O(1) time, so the whole operation takes O(n) + O(1) = O(n) time.
• at the end of the list — if we keep a reference to the last object, we can do this in O(1) time! Otherwise, we have to iterate through the entire array to find the last element. This will take O(n) time. Implementations of a link list typically include that reference to the last object to keep this operations quick.

Removing an element

• from the beginning — takes O(1). As with adding the element at the beginning of the list, we only need to change a few pointers.
• from anywhere else in the list — takes O(n) time. We have to find the element first (which will take O(n) time) and remove it. To remove the element C we change the value of B.next_element so that it points to D. That’s it.

---

That’s it! You know quite a lot about arrays and lists now. You should probably practice some interview questions!

In the third (and last) part, we’ll investigate why arrays can be significantly faster than linked lists when iterate through elements.

Thanks for reading!